Бывший российский математик доказал "недоступную" теорему,

Последовательность "синий-красный-красный-синий-красный-красный-синий-красный-красный" приведет в желтую вершину из любой другой вершины. Изображение Wikimedia Commons, созданное пользователем Quuxplusone.

63-летний израильский математик Авраам Трахтман (Avraham Trahtman), эмигрировавший в начале девяностых из России, доказал теорему, которая оставалась без доказательства 38 лет, сообщает газета The Jerusalem Post.

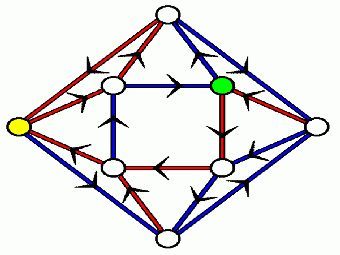
Доказательство будет опубликовано в Israel Journal of Mathematics. В настоящее время Трахтман работает в университете Бар-Илана, занимается алгеброй, конечными автоматами, формальными языками. Несколько лет после иммиграции Трахтман, однако, не мог устроиться по специальности, подрабатывал сторожем.

Теорема о раскраске дорог (Road colouring theorem/problem) была сформулирована израильскими математиками в 1970 году.

Упрощенное наглядное представление теоремы может выглядеть следующим образом: путешественник оказывается в лабиринте, ему нужно добраться до определенного места. От каждого перекрестка можно пойти по k дорогам, причем каждая дорога окрашена в один из k возможных цветов. Голос с неба может подсказать путешественнику последовательность цветов, которая укажет ему, по каким дорогам идти, чтобы достичь цели. Но голос с неба не знает, на каком перекрестке стоит путешественник, откуда он пойдет. Для некоторых типов лабиринтов возможна такая последовательность цветов, которая приведет путешественника к цели независимо от того, на каком перекрестке он стоит. Задача состоит в том, чтобы определить, для каких типов лабиринтов это возможно.

На иллюстрации приведен пример такого лабиринта: граф из восьми вершин, из каждой выходит по два ребра (в каждую также входит по два ребра, но идти можно только по исходящим, против стрелочки двигаться нельзя). Ребра окрашены в красный и синий цвет. Если путешественнику надо прийти в желтую вершину, голос с неба должен сказать ему "синий-красный-красный-синий-красный-красный-синий-красный-красный". Где бы ни стоял путешественник, пройдя по этой последовательности, он обязательно окажется в желтой вершине. Читатель может попробовать сам найти последовательность, гарантированно выводящую на зеленую вершину.

Формально теорема, доказанная Трахтманом, звучит следующим образом: каждый конечный сильно связный граф, все длины циклов которого взаимно просты и все вершины которого имеют одинаковое число исходящих ребер, имеет синхронизирующую раскраску. Теорема может применяться в теории графов, а также в теории конечных автоматов.